Le nombre d’or, également appelé Phi (φ), est une constante mathématique fascinante qui a captivé les mathématiciens, les artistes et les designers depuis des siècles. Le nombre d’or est souvent associé à la beauté, l’harmonie et l’équilibre, et il est présent dans de nombreux aspects de la nature et de la culture.

Dans cet article, nous allons explorer les propriétés du nombre d’or, sa relation avec la suite de Fibonacci, et comment le calculer en Python.

La définition du nombre d’or

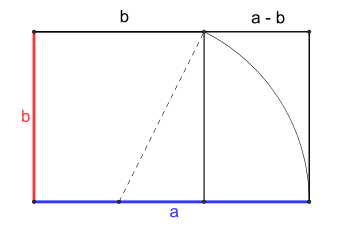
Le nombre d’or est défini tel que le rapport de la somme a + b des deux longueurs sur la plus grande est égal à celui de la plus grande sur la plus petite. En d’autres termes, si a est la plus grande quantité et b est la plus petite, le nombre d’or φ est donné par :

φ = (a + b) / a = a / b

Cela peut sembler compliqué, mais cela signifie simplement que le rapport entre a et b est égal à φ, et que la somme de a et b divisée par a est également égale à φ.

Propriétés du nombre d’or

Le nombre d’or possède de nombreuses propriétés intéressantes qui ont captivé les mathématiciens et les artistes depuis des siècles. Voici quelques-unes des propriétés les plus remarquables du nombre d’or :

• Le nombre d’or est irrationnel : cela signifie qu’il ne peut pas être exprimé comme le quotient de deux nombres entiers. Le nombre d’or est en fait un nombre transcendant, ce qui signifie qu’il ne peut pas être racine d’un polynôme à coefficients entiers.
• Le nombre d’or est aussi un nombre algébrique de degré deux, ce qui signifie qu’il est la solution positive de l’équation x² – x – 1 = 0.
• Le nombre d’or est approximativement égal à 1,61803398875… Il possède une expansion décimale infinie qui ne se répète jamais.
• Le nombre d’or est présent dans de nombreux aspects de la nature et de la culture, tels que les proportions du corps humain, les spirales de coquillages, les formes des cristaux, les motifs de croissance des plantes, et les compositions artistiques.

Relation entre le nombre d’or et la suite de Fibonacci

Le nombre d’or est étroitement lié à la suite de Fibonacci, car le quotient de deux termes consécutifs de la suite se rapproche de plus en plus de φ à mesure que les termes deviennent plus grands.

Plus précisément, si on prend le rapport entre chaque terme consécutif de la suite de Fibonacci, on obtient une séquence de nombres qui se rapproche de plus en plus de φ à mesure que les termes deviennent plus grands. Par exemple, le rapport entre les termes 55 et 34 est égal à 1,61764706, ce qui est très proche de φ.

Cette relation entre la suite de Fibonacci et le nombre d’or est importante car elle est présente dans de nombreux phénomènes naturels et artistiques, tels que les spirales de

coquillages, les motifs de croissance des plantes et les compositions artistiques. Cette relation peut être utilisée pour créer des designs et des compositions visuellement harmonieuses.

Calcul du nombre d’or en Python

Il existe plusieurs façons de calculer le nombre d’or en Python. Voici deux méthodes simples :

Méthode 1 : Calcul à partir de la définition

On peut calculer le nombre d’or à partir de sa définition en Python en utilisant simplement les opérations de base. Voici un exemple de code :

a = 1.0
b = 1.0 / a
phi = (a + b) / a
print(phi)

Ce code définit les variables a et b comme 1.0, puis calcule le nombre d’or φ en utilisant la définition φ = (a + b) / a. Le résultat est affiché à l’écran.

Méthode 2 : Calcul à partir de la suite de Fibonacci

On peut également calculer le nombre d’or en Python en utilisant la suite de Fibonacci. Voici un exemple de code :

a = 1
b = 1
for i in range(10):
    temp = b
    b = a + b
    a = temp
phi = float(b) / float(a)
print(phi)

Ce code utilise une boucle for pour calculer les dix premiers termes de la suite de Fibonacci, puis calcule le nombre d’or en utilisant le rapport entre les deux derniers termes.

Conclusion

Le nombre d’or est une constante mathématique fascinante qui possède de nombreuses propriétés intéressantes et est étroitement lié à la suite de Fibonacci. Le nombre d’or est présent dans de nombreux aspects de la nature et de la culture, et il peut être utilisé pour créer des designs et des compositions visuellement harmonieuses. En utilisant Python, il est facile de calculer le nombre d’or à partir de sa définition ou de la suite de Fibonacci.